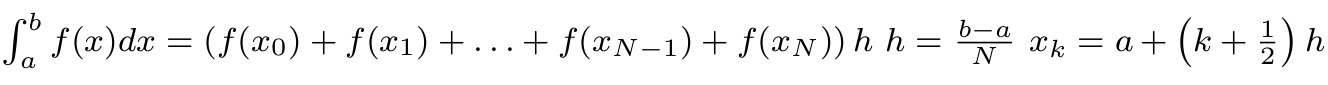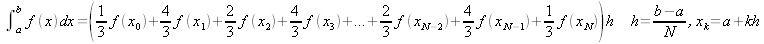|
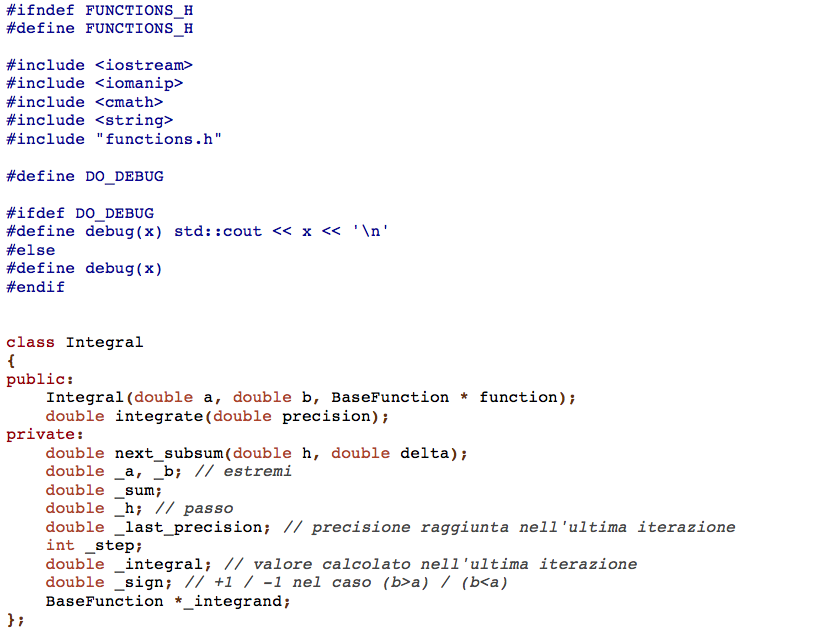
L'algoritmo è implementato all'interno di una classe che inizializza le variabili necessarie
all'algoritmo. Il costruttore prende in ingresso i valori estremi dell'intervallo e controlla
che siano in ordine. La condizione di uscita dell'algoritmo è basata sul confronto del risultato di due passaggi successivi. Se la differenza della stima dell'integrale tra due passaggi consecutivi è più piccola della precisione richiesta allora l'algoritmo si ferma. Questo poichè l'integrale calcolato su il raffinamento di una partizione è sempre una stima migliore dell'approssimazione con la partizione originaria. Nel costruttore calcoliamo la prima approssimazione: sum0 = (f[a] + f[b]) / 2; I0 = sum0 * (b-a)Al primo passaggio dell'algoritmo suddividiamo l'intervallo in due: sum1 = sum0 + f[x11]; I1 = sum1 * (b-a)/2e così secondo lo schema in figura  sum2 = sum1 + f[x21] + f[x22] ; I2 = sum2 * (b-a)/4 sum3 = sum2 + f[x31] + f[x32] + f[x33] + f[x34]; I3 = sum3 * (b-a)/8I valori dell'ultima approssimazione dell'integrale e dell'ultima somma calcolata sono memorizzati all'interno dell'oggetto. In questo modo, se viene richiesto di ricarcolare l'integrale, non è necessario ricominciare da capo. |