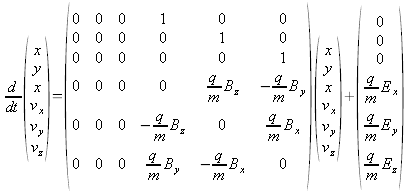|
Costruiamo una classe Differential che contiene per ora solo un metodo virtuale puro
Evaluate che si preoccupa di calcolare le derivate della funzione da integrare.
Tale classe dovrà contenere il metodo di Eulero ed il metodo di Runge-Kutta. L'header file della classe è quindi:  Sono quindi dichiarati il costruttore ed il distruttore ed i metodi Integrate e Draw per rappresentare in via grafica l'andamento della soluzione. Il costruttore riceve in ingresso il tempo massimo, tmax, fino a cui valutare la soluzione, il passo h e le condizioni iniziali x0. Sono anche dichiarati nell'area privata i metodi Evaluate ed Eulero che implementeranno il metodo di Eulero e valutaranno le derivate necessarie per la risoluzione del problema in esame con il metodo di Eulero. Nella classe è anche dichiarato, sempre nell'area privata, l'uso di TGraph di ROOT. La classe Oscillatore eredita dalla classe Differential e implementerà il metodo Evaluate proprio dell'equazione dell'oscillatore armonico. Inoltre sono dichiarati i metodi per definire la frequenza (SetFreq) e per richiamarla (GetFreq).  Riportiamo anche il main. 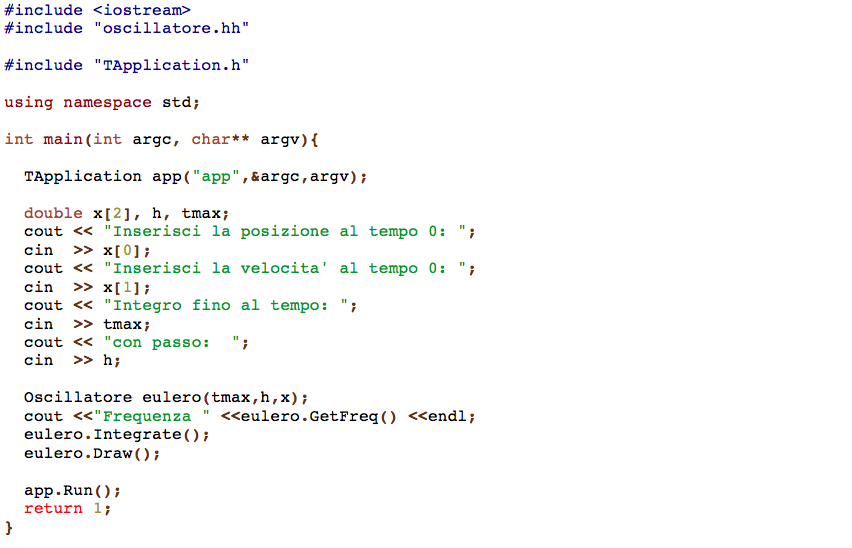 |