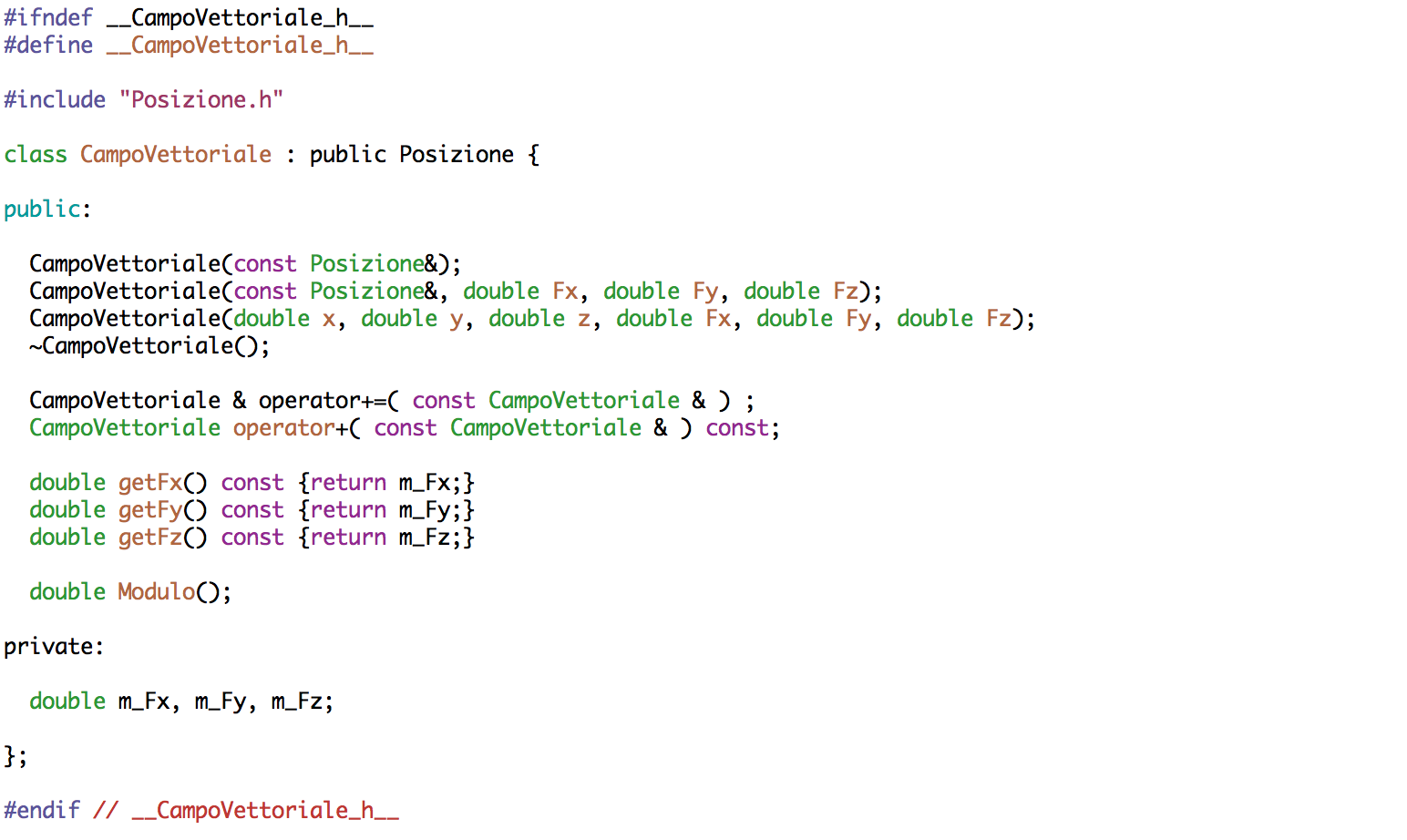
Nell'header file Posizione.h vanno dichiarati tutti i metodi ed i data membri. Si noti come i data membri siano tutti privati: questa modo di disegnare le classi implementa il concetto di incapsulamento e data hiding in C++.
Un paio di punti già che vale la pena ricordare:
|