Ricordiamo che in questo metodo l'approssimazione dell'integrale è definita dalla formula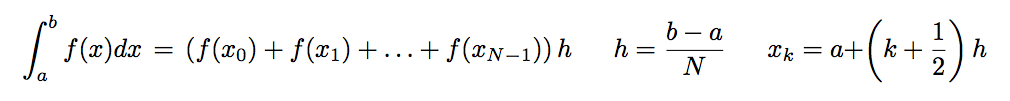 che fornisce un'accuratezza dell'integrale di O(h2). Notate che questo metodo non richiede il calcolo della funzione negli estremi di integrazione. |
| Lezione 7 Quadratura Numerica |
Simpson .
Come nell'esercizio 7.0
stampare una tabella ( o costruire un TGraph di ROOT) con la precisione raggiunta in funzione del numero di passi.