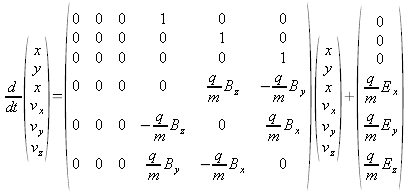L'equazione del pendolo è data dalla relazione
d2θ/dt2 = -(g/l)sinθ
dove g=9.8 m/s2 è l'accellerazione di gravità sulla superficie
terreste mentre l è la lunghezza del pendolo.
L'equazione differenziale si può approssimare con quella di un oscillatore armonico per piccole oscillazioni,
sinθ∼θ. In tal caso le oscillazioni risultano isocrone cioè, con periodo indipendente
dall'ampiezza delle oscillazioni.
Questa però è solo un'approssimazione, e per grandi oscillazioni bisogna usare l'equazione esatta. Essendo il moto non più armonico, il periodo di oscillazione dipende dall'ampiezza della stessa.
La figura illustra il periodo al variare dell'ampiezza per un pendolo con l=1 m:
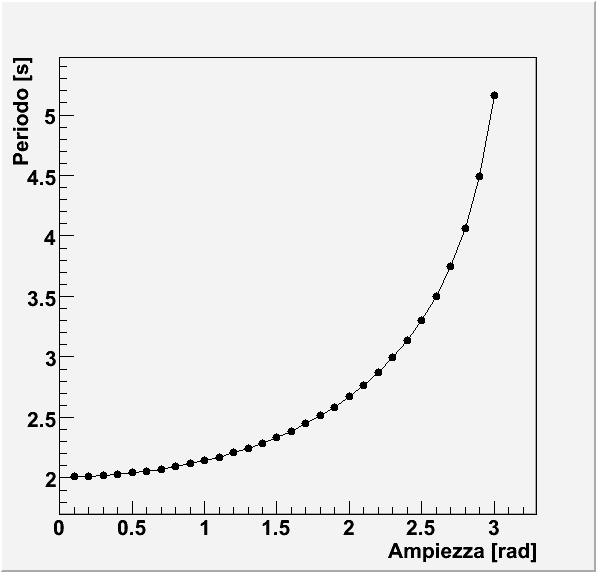
si noti come per piccole oscillazioni, il periodo sia effettivamente quello atteso
dall'approssimazione dell'oscillatore armonico:
T=2π/√(g/l)=2.007 s,
ma aumenti significativamente per grandi ampiezze.
|
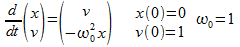

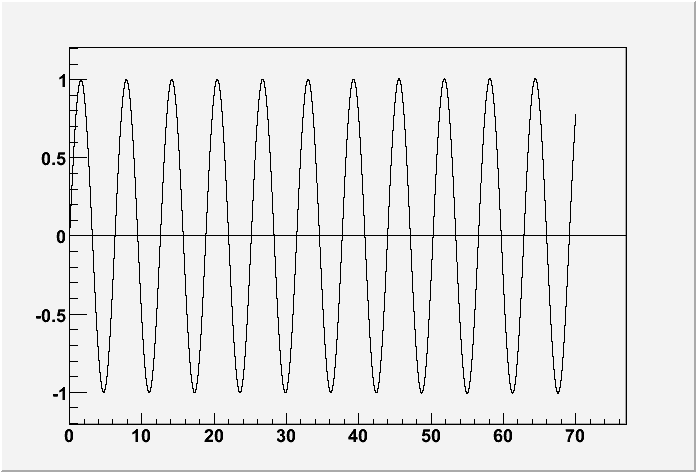
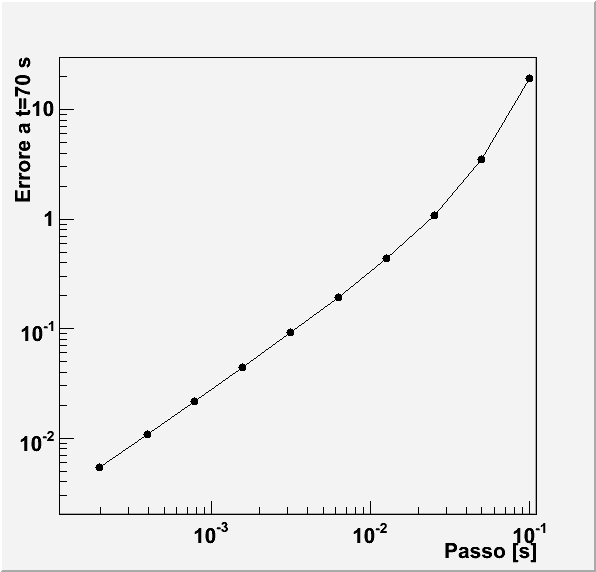
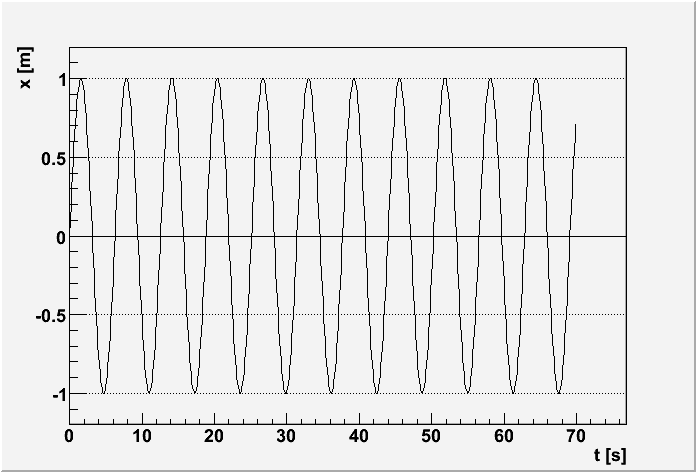
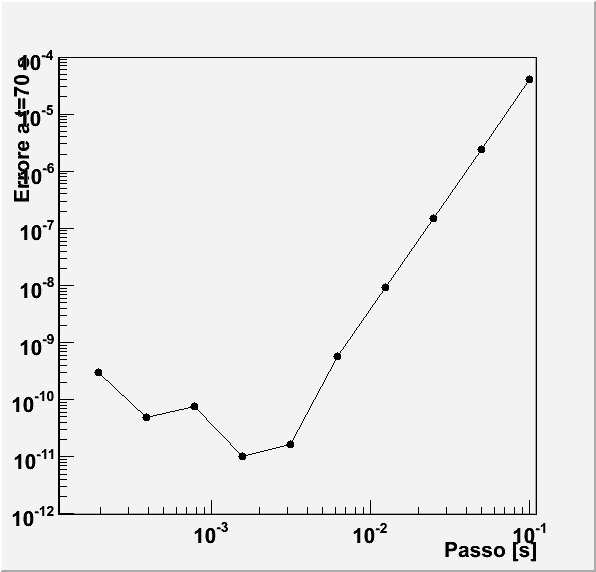

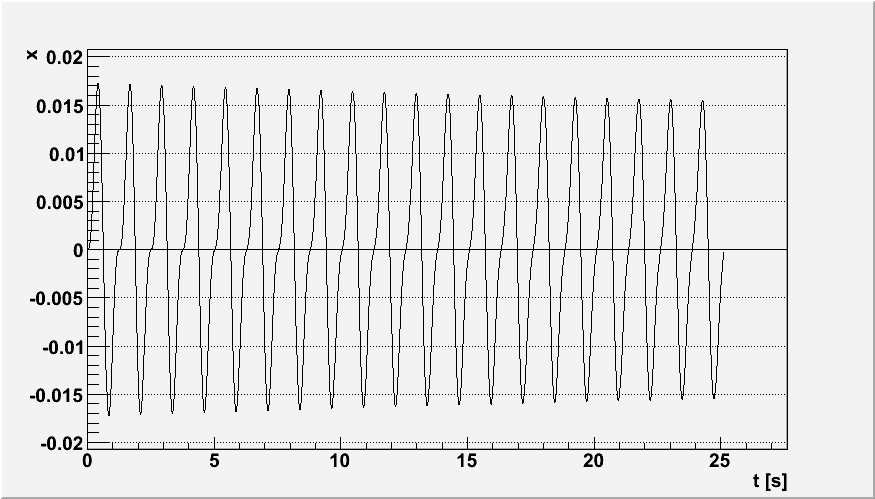 ω=5 rad/s
ω=5 rad/s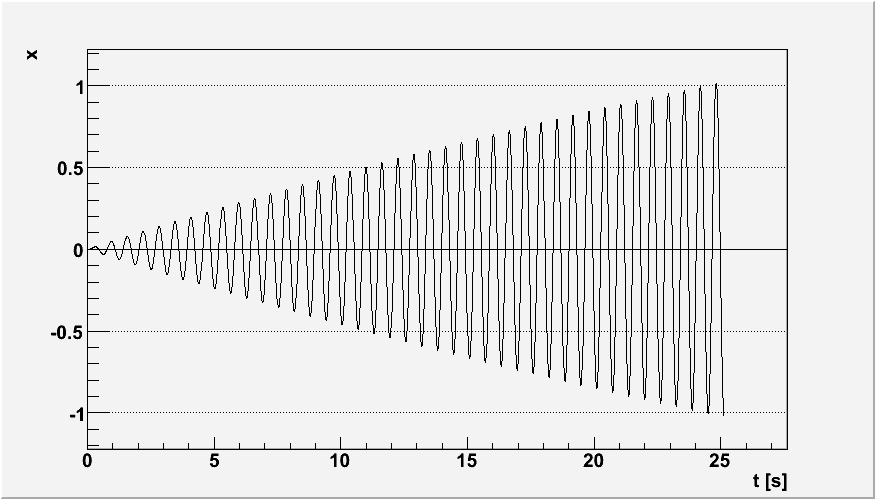 ω=10 rad/s
ω=10 rad/s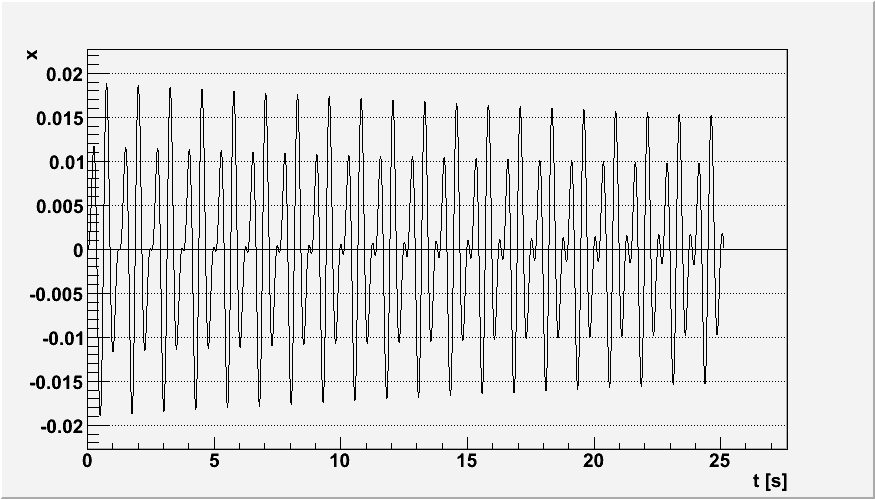 ω=15 rad/s
ω=15 rad/s