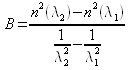ESERCIZIO
11.0 - Simulazione dell'esperienza dello spettrometro a prisma (da consegnare)
(da
consegnare):
La dipendenza dell'indice di rifrazione dalla lunghezza d'onda della luce incidente viene descritta dalla legge di Cauchy:
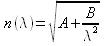
L'esperienza dello spettrometro a prisma si propone di misurare l'indice di rifrazione del materiale di un prisma per le diverse lunghezze d'onda di una lampada al mercurio onde determinare i parametri A e B che caratterizzano tale materiale.
L'apparato sperimentale consiste in un goniometro sul quale viene posizionato il prisma. Una lampada a vapori di mercurio viene posizioneta da un lato del canocchiale con due collimatori per produrre un fascio luminoso che incide sul prisma. Il fascio di luce riflesso o rifratto viene osservato tramite un altro canocchiale. Gli angoli corrispondeni all'orientamento del supporto sul goniometro ed alla posizione dei canocchiali sono leggibili su di un nonio.

La nostra simulazione consiste nell'assumere dei valori verosimili dei parametri della legge di Cauchy, vedere
come questi si traducono in quantità osservabili e stimare se la nostra procedura di misura e di analisi dei dati ci permette di derivare correttamente i valori utilizzati come ingresso nella simulazione e con quale incertezza.
Nell'esperimento l'unico tipo di grandezze misurate sono gli angoli, per cui possiamo assumere un'incertezza uguale per tutte le misure angolari e pari a σθ=0.3 mrad.
Nell'esperienza di laboratorio, l'angolo di apertura del prisma α=60o ed il materiale del prisma ha valori dei parametri di Cauchy A=2.7, B=60000 nm2.
Consideriamo le due lunghezze d'onda estreme della lampada al mercurio, il giallo, λ1=579.1 nm, ed il viola, λ2=404.7 nm.
La misura sperimentale consiste nella determinazione:
- dell'angolo corrispondente al fascio non deflesso in assenza del prisma: θ0.
- dell'angolo corrispondente alla deviazione minima della riga del giallo:
θm(λ1).
- dell'angolo corrispondente alla deviazione minima della riga del viola:
θm(λ2).
L'analisi dati consiste nella seguente procedura:
- determinazione degli angoli di deviazione minima:
δm(λ1)=θm(λ1)-θ0.
δm(λ2)=θm(λ2)-θ0.
- calcolo degli indici di rifrazione n(λ) dalla relazione:
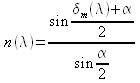 .
.
- calcolo dei parametri A e B dalle formule:
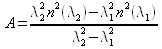
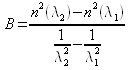
Parte I
Costruire una classe EsperimentoPrisma con le seguenti caratteristiche:
- come data membri deve avere sia i valori veri che i valori misurati di tutte le quantità ed in più un generatore di numeri casuali
RandomGen (vedi lezione 10);
- nel costruttore deve definire tutti i valori di ingresso delle quantità
misurabili a partire dai
parametri A, B ed α e dalle lunghezze d'onda;
N.B.: il valore di θ0 è arbitrario, ma,
una volta definito, i θm sono fissati.
- un metodo
Esegui() che effettua la misura sperimentale e determina dei valori misurati
di θ0, θm(λ1),
θm(λ2);
N.B.: il valore misurato di un angolo si ottiene estraendo un numero distribuito
in maniera gaussiana intorno al suo valore di ingresso nella simulazione
e deviazione standard σθ.
- i metodi necessari per accedere ai valori dei data membri, sia quelli di ingresso che quelli misurati..
Scrivere un programma che esegua 10000 volte l'esperimento, faccia un istogramma dei valori misurati, e calcoli media e deviazione standard di tali valori.
N.B.: Per il calcolo di medie e varianze potete decidere di immagazzinare i dati in un contenitore (std::vector o Vettore e utilizzare le funzioni sviluppate nelle prime lezioni oppure accedervi direttamente dagli istogrammi di ROOT come mostrato qui (ricordandosi di aggiungere histo.StatOverflows( kTRUE ); in modo da forzare l'utilizzo di eventuali underflow e overflow per calcoli statistici).
Parte II
Aggiungere alla classe un metodo Analizza() che faccia i calcoli relativi all'analisi dati ed estendere il programma in modo da eseguire l'analisi dati dei 10000 esperimenti e fare istogrammi di:
- differenza tra i valori misurati e quelli attesi di δm(λ1) e δm(λ2), quello bidimensionale delle differenze per le due lunghezze d'onda, e calcolare il coefficiente di correlazione.
- differenza tra i valori misurati e quelli attesi di n(λ1) e n(λ2), quello bidimensionale delle differenze per le due lunghezze d'onda, e calcolare il coefficiente di correlazione.
- differenza tra i valori misurati e quelli attesi di A e B, quello bidimensionale delle differenze, e calcolare il coefficiente di correlazione.
In tutti i casi, se possibile, confrontate il risultato della simulazione con quello ottenuto dalla propagazione degli errori.
Brevi Richiami
La classe EsperimentoPrisma
La classe EsperimentoPrisma deve contenere al suo interno un generatore di numeri casuali
per la simulazione del processo di misura, tutti i parametri che definiscono l'esperimento
e, per le quantità misurate, sia il valore assunto nella simulazione, che il valore ottenuto dal processo
di esecuzione ed analisi dati dell'esperimento.
Il suo header file, potrà pertanto essere del tipo:

N.B.: in questo header mancano i metodi tipo Get per accedere ai data membri.
La configurazione dell'esperimento, con il calcolo di tutti i valori assunti per le quantità
misurabili, può venire fatta nel costruttore di default della classe, che in questo caso
risulta più complicato del solito:

Notate l'uso della lista di inizializzazione nel costruttore: questa permette di inizializzare direttamente i valori dei data membri anzich` procedere all'assegnazione dei valori nel costruttore dopo che i data membri siano stati costruiti. Nel nostro caso particolare diventa utile per inizializzare l'oggetto m_rgen invocando il costruttore opportuno ( altrimenti avrebbe usato il costruttore senza argomenti che nel nostro caso non esiste ). Potete trovare una buona spiegazione dell'utilizzo delle liste di inizializzazione in qui.
|
Istrogrammi bidimensionali
Per verificare le correlazioni tra due variabili, è utile utilizzare istogrammi bidimensionali,
in cui i canali sono definiti da range di valori sia di una variabile che dell'altra
Per costruire questi istogrammi, utilizzeremo la classe
TH2F
Questa ha un costruttore che premette di dividere in canali sia la coordinata x che la y dell'istogramma:
TH2F::TH2F(char* nome, char* titolo, int canali_x, double xmin, double xmax, int canali_y, double ymin, double ymax);
La classe TH2F ha gli stessi metodi Fill e Draw della classe TH1F, l'unica differenza è che ora Fill ha bisogno della coppia completa di valori per decidere il canale in cui viene collocato l'evento:
TH2F::Fill(double x, double y);
|
Calcolo del coefficiente di correlazione
Il coefficiente di correlazione ρ tra due variabili x e y, può venire espresso
come:
(<xy> - <x> <y>)/σxσy
Si noti che dalla relazione:
σ2x = <x2>-<x>2
risulta che può essere più conveniente nel ciclo di esperimenti calcolare le sommatorie di
x, y, x2, y2 e xy, ed al termine del ciclo
effettuare le medie e trovare incertezze e correlazioni. Il tutto non richiede strettamente di
immagazinare tutti i dati dei 10000 esperimenti.
|
Risultati attesi
|
Nella seguente tabella sono riportati i valori numerici attesi per le varie quantità ed i grafici ottenuti
per una simulazione. Si noti come le varie quantità sono fortemente correlate.
|
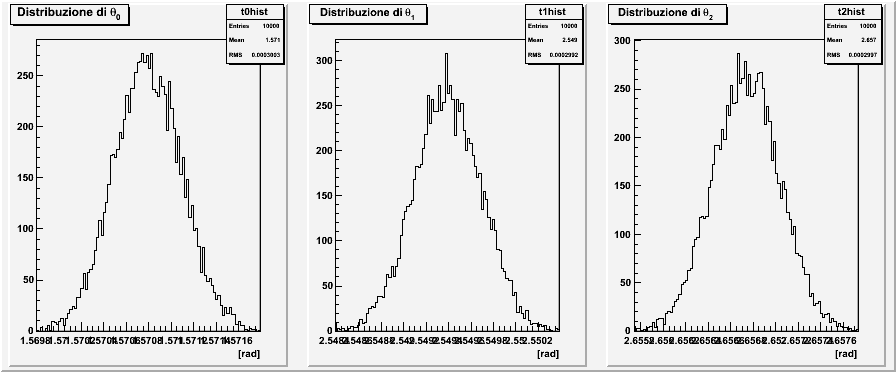
θ0 = 1.5708 (arbitrario)
θ1 = 2.5494 (conta solo la differenza
θ2 = 2.6567 rispetto a θ0)
σ(θi) = 0.0003 (i=0,1,2)
| 
|
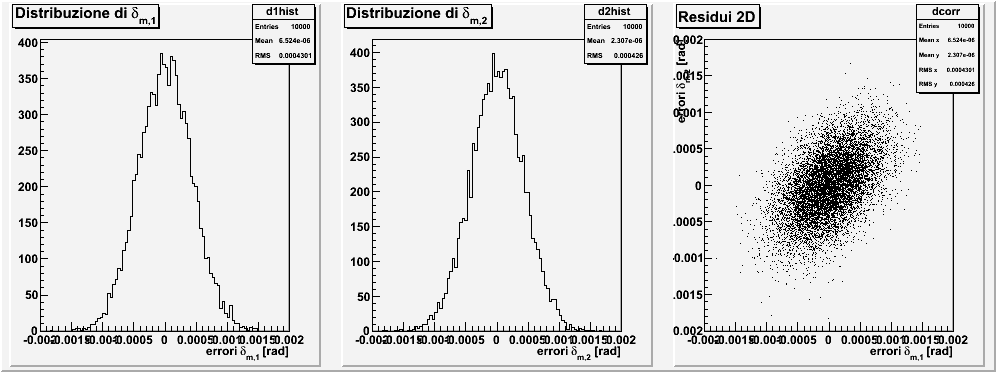
δm,1 = 0.97860 rad
δm,2 = 1.08594 rad
σ(δm,i) = 0.00043 rad (i=1,2)
ρ(δm,1,δm,2) = 50%
| 
|
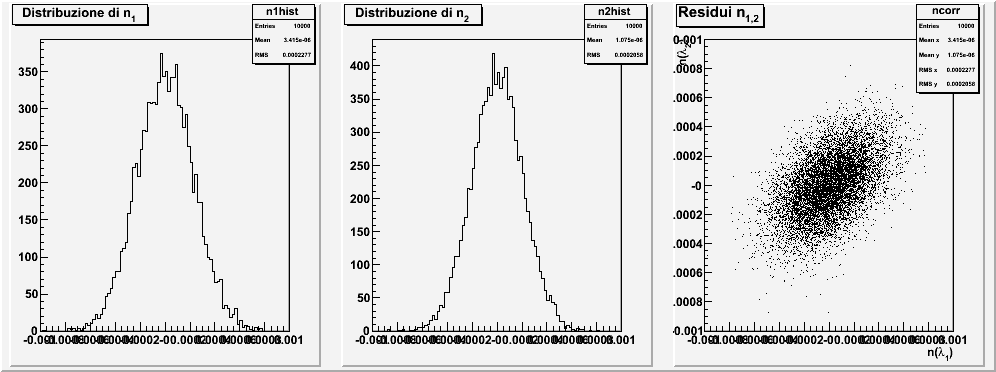
n1 = 1.69674
σ(n1) = 0.00022
n2 = 1.75110
σ(n2) = 0.00021
ρ(n1,n2) = 50%
| 
|
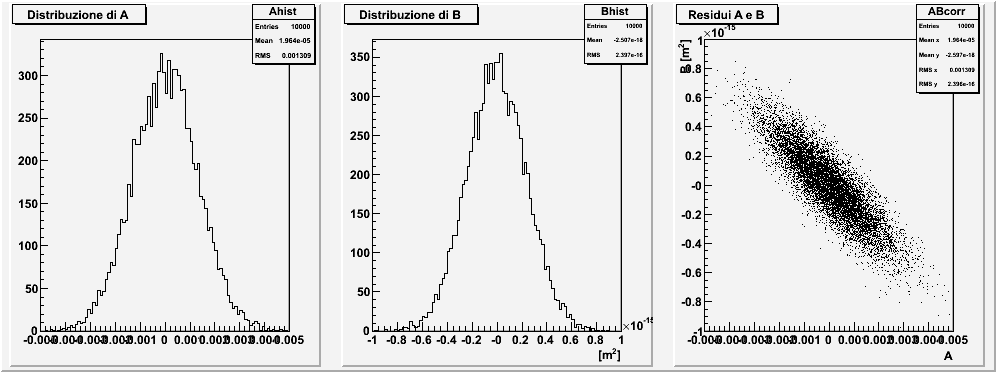
A = 2.70002
σ(A) = 0.0013
B = 60000 nm2
σ(B) = 240 nm2
ρ(A,B) = -87%
| |
ESERCIZIO
11.1 - Attrito viscoso (facoltativo)
:
Svolgere il tema d'esame sulla simulazione di un esperimento per la misura della viscosità di un materiale:
preappello del gennaio 2009, esercizio 6

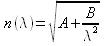

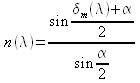 .
.